Clinical applications of the areas under ESPVR

Indexes of cardiac performance

It has long been observed that the use of the ejection fraction (EF) to assess the condition of the heart offers serious limitations (1). It is estimated that half of the patients presenting with symptoms of cardiomyopathies and heart failure (HF) have preserved EF defined as EF >50%. It was shown in (2) that the areas under the end-systolic pressure-volume relation (ESPVR) in the heart ventricles are sensitive indexes to reflect the state of the myocardium, a review of some clinical applications of indexes derived from the ESPVR can be found in (3). An objective of the study by Doyle et al. (4) is precisely to show that areas under the ESPVR, or bivariate combination of areas with another index, can be used as a prognostically useful tool for studying cases of women with suspected myocardial ischemia.

The ESPVR is the relation between pressure and volume in the left or right ventricle when the myocardium reaches its maximum state of activation near end-systole (2,3). There have been several studies on the ESPVR (3,5-7), most of these studies have focused on the use of the maximum slope E_max and the volume axis intercept V_om of the ESPVR in order to assess the state of the myocardium. Because of the difficulty to calculate V_om, some researchers have tried to neglect V_om and to approximate E_max ≈ (end-systolic pressure/end-systolic volume) (4). Such an approximation can only be justified if it is proven that the results obtained contain useful reliable clinical information. In what follows we introduce some relations that reflect the way the energetic of cardiac contraction is related to the areas under the ESPVR, and how the EF is also influenced by these areas. It may provide some background for the study published in (4).

Mathematical formalism

PVR

As in previous publications (8-11), the left ventricle is represented as a thick-walled cylinder contracting symmetrically (Figure 1). A radial active force D_r (force per unit volume of the myocardium) is developed by the myocardium during the contraction phase. The active pressure on the inner surface of the myocardium (endocardium) is given by ∫_a^b D_r dr=P_iso, where a = inner radius of the myocardium, b = outer radius of the myocardium. We neglect inertia and viscous forces since they are relatively small. The equilibrium of forces on the endocardium can then be expressed in the form:

P_iso–P = E (V_ed–V)          [1]

Figure 1 Left ventricle represented by the cross-section of a thick-walled cylinder. D_r, active radial force/unit volume of the myocardium; P, left ventricular pressure; P_o, outer pressure (assumed zero) on the myocardium; a, inner radius; b, outer radius; h = b - a = thickness of the myocardium

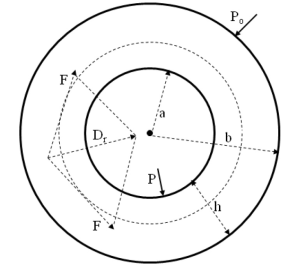
P is the left ventricular pressure, V is the corresponding left ventricular volume, V_ed is the end-diastolic volume (the largest volume when dV/dt =0). The right-hand side of Equations [1] is the pressure on the endocardium resulting from the elastic deformation of the myocardium. When the elastance E reaches its maximum value E_max near end-systole (maximum state of activation of the myocardium), we can write Equations [1] as follows:

P_isom–P_m = E_max (V_ed–V_m)          [2]

We take V_m ≈ V_es the end-systolic volume when dV/dt = 0.

ESPVR

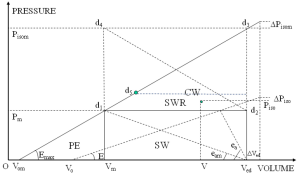
Equations [1] and [2] are represented graphically in a simplified way in Figure 2. The ESPVR is a relation between P_m and V_m when the peak isovolumic pressure P_isom is kept constant, it is represented by the line d₃V_om with slope E_max.

During a normal ejecting contraction the PVR is represented by the rectangle V_edd₂d₁V_m. Equations [2] can be split into the following form:

P_m = E_max (V_m–V_om)          [3]

P_isom = E_max (V_ed–V_om)          [4]

We can distinguish the following cases described by the ratio E_max/e_am (maximum ventricular elastance/maximum arterial elastance) and the stroke volume SV ≈ V_ed–V_m (see Figure 2).

(I) Normal physiological state of the heart, with d₁ below d₅ on the line d₃V_om. In this case we have SV > (V_ed–V_om)/2, with E_max/e_am ≈2 and P_isom/P_m ≈3. This case corresponds to maximum efficiency for O₂ consumption by the myocardium.

(II) Mildly depressed state of the heart, with d₁ and d₅ coinciding. In this case we have SV ≈ (V_ed–V_om)/2, with E_max/e_am ≈1 and P_isom/P_m ≈2. The stroke work SW reaches its maximum value SW_max.

(III) Severely depressed state of the heart, with d₁ above d₅ on the line d₃V_om. In this case we have SV ed–V_om)/2, with E_max/e_amisom/P_m

Notice from Figure 2 that in cases (II) and (III) an increase in pressure P_m causes a decrease of the stroke work SW, resulting in cardiac insufficiency.

Experimental verification of these results can be found in (5) (left ventricle) and in (6) (right ventricle) for experiments on dogs, and in (7) for results obtained from patients.

We have the following areas under the ESPVR:

(I) SW = P_m (SV), energy delivered to the systemic circulation;

(II) PE = P_m(V_m–V_om)/2, potential energy apparently related to the internal metabolism of the myocardium;

(III) CW = (P_isom–P_m) SV/2, energy apparently absorbed by the passive medium of the myocardium;

(IV) SWR = SW_max–SW, stroke work reserve. It is the reserve energy that can be delivered to the systemic circulation when afterload represented by P_m is increased.

We have SW + PE + CW = TW the total area under ESPVR. One can derive the following relation for the stroke volume:

SV = (CW/TW)^1/2 (V_ed –V_om)          [5]

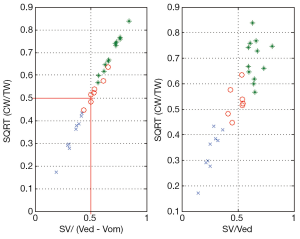
Which shows how SV (and EF = SV/V_ed) is determined by the areas under the ESPVR. When CW/TW = 1/4 (d₁ and d₅ coincide in Figure 2), we get from Equations [5] SV = (V_ed-V_om)/2. Experimental verification is shown in Figure 3. We also have:

E_max/e_am =2×CW/SW          [6]

Figure 2 Simplified PVR in the left ventricle, V_edd₂d₁V_m represents the pressure-volume loop in a normal ejecting contraction (area SW). The ESPVR is represented by the line d₃V_om with midpoint d₅ and slope E_max, the line with slope E is an intermediate position. The left ventricular pressure P_m is assumed constant during the ejection phase. The changes ΔP_iso and ΔP_isom correspond to ΔV_ed according to the Frank-Starling mechanism

Figure 3 Graphical verification of [5] (left side), and similar relation with the EF = SV/V_ed (right side). Experimental data taken from Asanoi et al. (7). Data correspond to three clinical groups: (I) EF≥60% ‘*’; (II) 40%

---

Acknowledgements

Disclosure: The author declares no conflict of interest.

---

References

1. Sanderson JE. Heart failure with a normal ejection fraction. Heart 2007;93:155-8. [PubMed]
2. Crottogini AJ, Willshaw P, Barra JG, et al. Inconsistency of the slope and the volume intercept of the end-systolic pressure-volume relationship as individual indexes of inotropic state in conscious dogs: presentation of an index combining both variables. Circulation 1987;76:1115-26. [PubMed]
3. Burkhoff D, Mirsky I, Suga H. Assessment of systolic and diastolic ventricular properties via pressure-volume analysis: a guide for clinical, translational, and basic researchers. Am J Physiol Heart Circ Physiol 2005;289:H501-12. [PubMed]
4. Doyle M, Weinberg N, Pohost GM, et al. Left ventricular energy model predicts adverse events in women with suspected myocardial ischemia: results from the NHLBI-sponsored women’s ischemia syndrome (WISE) study. Cardiovasc Diadn Ther 2013;3:64-72.
5. Burkhoff D, Sagawa K. Ventricular efficiency predicted by an analytical model. Am J Physiol 1986;250:R1021-7. [PubMed]
6. Brimioulle S, Wauthy P, Ewalenko P, et al. Single-beat estimation of right ventricular end-systolic pressure-volume relationship. Am J Physiol Heart Circ Physiol 2003;284:H1625-30. [PubMed]
7. Asanoi H, Sasayama S, Kameyama T. Ventriculoarterial coupling in normal and failing heart in humans. Circ Res 1989;65:483-93. [PubMed]
8. Shoucri RM. Theoretical study of pressure-volume relation in left ventricle. Am J Physiol 1991;260:H282-91. [PubMed]
9. Shoucri RM. Ventriculo-arterial coupling and the areas under the end-systolic pressure-volume relation. Jpn Heart J 1997;38:253-62. [PubMed]
10. Shoucri RM. Studying the mechanics of left ventricular contraction. IEEE Eng Med Biol Mag 1998;17:95-101. [PubMed]
11. Shoucri RM. ESPVR, ejection fraction and heart failure. Cardiovasc Eng 2010;10:207-12. [PubMed]

Cite this article as: Shoucri RM. Clinical applications of the areas under ESPVR. Cardiovasc Diagn Ther 2013;3(2):60-63. doi: 10.3978/j.issn.2223-3652.2013.05.05