
MRI-based comprehensive analysis of vascular anatomy and hemodynamics
Introduction
As an advancement of 2D phase contrast MRI techniques (1), four-dimensional phase contrast (4D Flow) flow mapping has emerged as a rich source for assessment of hemodynamics (2-4). Post-processing of 4D Flow MRI allows measuring several quantitative features that characterize the secondary flow patterns in the aorta and pulmonary artery (5-18). Turbulence, helical flow patterns, eccentricity and other secondary flow patterns are associated with many cardiovascular diseases (5-12). The impact of turbulent flow patterns on hemodynamics and blood vessel walls has been recognized long before cardiac MRI (CMR) became clinically available (13). Turbulence negatively affects the red blood cells (RBCs) and endothelial cells, and plays an important role in thrombogenesis and plaque formation (14,15). Flow eccentricity—quantified by flow displacement—is associated with aortic dilatation and may serve as predictor for the development of aneurysms (10).
Reduction of secondary flow patterns and related clinical complications plays an important role in optimization of surgical procedures (19-21). In particular, detection of pairs of counter-rotating vortices, referred to as the Dean flow patterns (22) as well as vortices with retrograde flow, have been used as markers to validate and compare different types of sinus prostheses for aortic root replacement (23) mainly based on visual streamline analyses. A quantitative computational assessment of vortices using corresponding parameters such as circulation or helicity density may impede the detection of Dean flow patterns due to cancellation of counter-rotating vortices.
To comprehensively assess cardiovascular hemodynamics, advanced post-processing techniques are essential for analysis of 4D Flow MRI. Many clinical 4D Flow MRI studies have implemented semi-quantitative grading schemes to characterize secondary flow patterns such as vortical or helical flow (23). These studies have emphasized on the importance of a quantitative analysis tool for flow patterns and their relationship to vascular anatomy. Moreover, the computational costs to analyze a large number of quantities usually discourage the use of these parameters for clinical decision making given the limited computing resources in clinical settings. Consequently, a method that can attain and process a large quantity of hemodynamic and anatomic characteristics at a relatively low computing cost is highly desirable.
We describe a methodological workflow for comprehensive analysis of vascular anatomy and hemodynamics based on 4D Flow MRI. This workflow includes the definition of a multi-dimensional feature space built from a few complementary building blocks to determine a large number of anatomic and hemodynamic parameters within a blood vessel. We also present instructions for quantification of Dean flow patterns. This article is presented according to the MDAR reporting checklist (available at http://dx.doi.org/10.21037/cdt-20-767).
Methods
A 4D Flow analysis platform was developed using the medical image processing and visualization framework MeVisLab (Mevis Medical Solutions, MeVisLab version 2.8.2). We processed 4D Flow MRI data of three exemplary test cases: a normal control (51-year-old female subject), a pathologically-shaped neo-aorta in a patient with hypoplastic left heart syndrome (HLHS) two years after completion of the Fontan circulation (11-year-old male subject) (24), and the aorta of a patient after surgical correction of the aortic root aneurysm by Valve-Sparing Aortic Root Replacement (VSARR) with sinus prosthesis (61-year-old male subject). Analysis of turbulent energy was performed only for the HLHS patient. The data of the normal control subject and the VSARR patient were used to quantify Dean flow pattern. The post-processing of data was performed on an iMac computer with 3.5 GHz Intel Core i9 processor with 32 GB RAM. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013) and was approved by institutional ethics board of Kiel University’s Faculty of Medicine (A168/07) with informed consent taken from all individual participants.
Workflow
The methodological workflow implemented in the analysis platform is illustrated in Figure 1 and described in detail below. For determination of inter-observer variability, two independent observers analyzed the data.
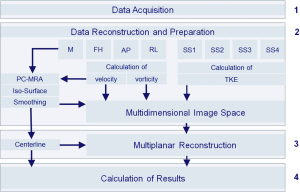
Data acquisition
Our method uses 4D Flow MRI data and provides post-processing according to common guidelines (25). For the test cases, CMR data were acquired on a 3.0 Tesla MR systems (Philips Healthcare, Best, Netherlands). The slab of the measurement covered the aorta from the aortic arch down to the diaphragm.
Data reconstruction, calculation of feature space, and segmentation
Data reconstruction
Seven datasets were reconstructed covering the time-resolved collection of CMR data: four datasets comprising magnitude data [1–4], one with velocity-compensation, i.e., no velocity sensitivity S0 [1] and three datasets with velocity encoding along the three spatial directions S1, S2, S3 [2–4], as well as three datasets for phase contrast data with velocity-encoding along the three spatial directions [5–7]. Correction of phase offset errors was performed on the MR scanner by a local phase correction (LPC) filter provided by the manufacturer to subtract the phase offsets due to the eddy currents and concomitant gradients, referred to as Maxwell terms.
Composition of feature space
A 7-dimensional feature space was assembled from velocity (3-dimenional), vorticity (3-dimensional) and turbulent kinetic energy density (1-dimensional). Vorticity was computed from the velocity vector field υ(r,t) with r and t referring to a vector with the spatial coordinates in time, respectively:
where (or nabla operator) is the discrete vector differential operator numerically approximated with the central differencing scheme (26). Turbulent kinetic energy density (TKE) was calculated from the magnitude data in the four scan segments, S0, S1, S2, S3 (5-8,27,28) such that:
Segmentation
Segmentation of the blood vessel of interest was performed as follow: a Phase Contrast Magnetic Resonance Angiography (PC-MRA) was reconstructed from the product of absolute velocity and average magnitude (S0+S1+S2+S3)/4 of the four scan segments averaged over all cardiac time frames. An iso-surface was calculated from the PC-MRA by applying a neighboring cells algorithm based on a user-defined threshold (29). The volume included in the iso-surface was used as the segmented volume.
Curved multiplanar reconstruction (MPR)
A curved MPR (30) of the multi-dimensional image data was performed in perpendicular planes spaced at equal distance increments of 1 mm along the blood vessel’s centerline. Anatomical landmarks were placed at the vessel’s cross-sectional center point using anatomic slice images (magnitude). A curved vessel centerline was defined as the natural cubic spline through the landmarks. To accomplish the above steps, a graphical user interface (GUI) was developed for 3D visualization of segmentation, centerline definition and MPR planes overlaying on top of the rendered anatomy. Visualization of the center line was performed in real-time to facilitate users defining and modifying the landmarks as needed. Image data were then resampled by projection into the planes using trilinear interpolation, a three-dimensional linear interpolation among the neighboring 8 voxels (31). The MPR resampling was limited to the segmented region. For example, an MPR plane in the ascending aorta may still intersect with the descending aorta. In our test cases, resampling was limited to a circular region around the aortic center with the diameter of 30 mm, just slightly above the maximum diameter of the aorta (28 mm). This parameter must be adjusted for each acquisition. Due to the multi-dimensional nature of the image data, the trilinear interpolation was performed multi-dimensionally, and thus each pixel in the resampled planes corresponds to a point in the 7-dimensional feature space. After MPR, velocity, vorticity, and turbulent kinetic energy density were overlaid on each cross-sectional MPR plane.
Model’s outputs
Results were based on the data of the resampled MPR planes and centerline. The resampled MPR planes were comprised of information of vascular hemodynamics as well as the cross-sectional anatomic information at a given position and time. As an important byproduct of the MPR, the centerline is used as the source for anatomic information about the vessel.
Computation of hemodynamics parameters and cross-sectional area: quantities related to vascular hemodynamics as well as the cross-sectional area were computed for each MPR plane position at each time frame.
(I) The vessel’s cross-sectional area (A) was calculated from the sum of pixels in the MPR plane. The equivalent blood vessel diameter (d) was derived from the cross-sectional area according to
(II) Flow rate was calculated from the velocity field according to
Forward Qfwd=Q+ and backward Qbwd=Q- components of the flow rate were calculated by considering exclusively positive (+) and negative (−) contributions.
(III) The retrograde flow fraction was calculated from the flow components according to
(IV) Circulation, as the fluid dynamics parameter that quantifies rotations in the cross sectional area was computed as (32):
Circulation was independently calculated for positive (+) and negative (−) contributions corresponding to clockwise Γ+ and anti-clockwise Γ- rotations. Clockwise and anti-clockwise rotation refer to the direction of rotation observed considering forward direction. The magnitude of circulation was obtained by re-combining clockwise and anti-clockwise contributions:
(V) The asymmetry of clockwise and anti-clockwise circulation was quantified according to
(VI) Helicity density as a fluid dynamics’ parameter that quantifies the flow helical pattern, was computed from the distributions of velocity and vorticity in the cross-sectional area:
Helicity density is defined as helicity (33) per lumen volume, and in contrast to helicity, it is not explicitly depending on the size of the lumen volume. Helicity density was calculated considering the positive (+) and negative (−) contributions in conjunction with the velocities in forward (fwd) and backward (bwd) directions , , , and re-combined to obtain clockwise and anti-clockwise components. The magnitude of helicity was obtained by re-combining clockwise and anti-clockwise contributions:
(VII) The asymmetry of clockwise and anti-clockwise helicity was calculated according to
(VIII) The angle between velocity and vorticity vectors is referred to as the ‘relative helicity’ density (33):
(IX) Turbulent kinetic energy density (27,28) in the MPR plane was computed by averaging the turbulent kinetic energy density over the cross-sectional area
(X) Flow displacement (9) as the fluid dynamics parameter that quantifies the eccentricity of vascular flow in the cross-sectional area is defined as the distance between the center of velocity and the centroid of the lumen and was calculated as fraction of the vessel diameter d according to
where r is the position in the cross-sectional area.
Computation of curvature, torsion and effective torsion from the centerline: in our test cases, the path of the centerline was divided into segments of 1 mm length defined by a segment vector , the arc length , and a unit tangent vector . Curvature and torsion are defined according to
and
where as the principle normal vector and the binormal vector are unit vectors. Thereby, curvature (and torsion) is defined in units of the inverse length (L-1). According to the sign convention used in Eqs. [9] and [10], positive torsion corresponds to a helix with clockwise rotation (right-handed helix) and negative torsion corresponds to a helix with anti-clockwise rotation (left-handed helix). The curvature-weighted torsion κ·τ is referred to as ‘effective torsion’.
Results
All datasets were processed with an average post-processing computation time of 8±2 minutes. Quantitative results on the normal control subject, HLHS patient and VSARR patient are presented in Figures 2-5 and in Table 1.
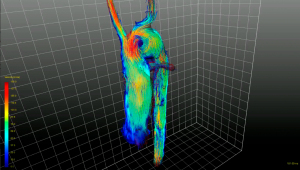
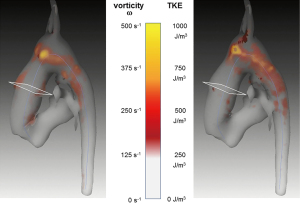
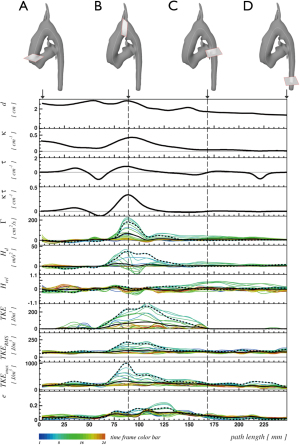
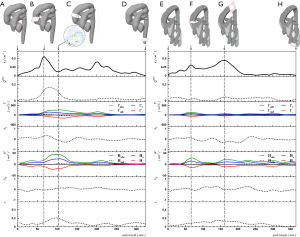
Table 1
| Parameter | Normal control | HLHS patient | VSARR patient | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Value | Inter-observer variability | Location | Value | Inter-observer variability | Location | Value | Inter-observer variability | Location | |||
| Aortic length (mm) | 366 | 0.5% | 248 | 2.7% | 323 | 1.0% | |||||
| Highest position of aortic arch (mm) | 149 | 1.3% | 94 | 6.4% | 179 | 3.6% | |||||
| Average diameter d (mm) | 30 | 3.3% | 21 | 3.7% | 29 | 4.7% | |||||
| Peak curvature κ (1/cm) | 0.45 | 3.2% | 160 | 0.53 | 0.3% | 87 | 0.55 | 2.9% | 67 | ||
| Peak eff torsion κτ (1/cm2) | 0.16 | 12.6% | 103 | 0.41 | 3.5% | 86 | 0.38 | 1.1% | 55 | ||
| Peak QRFF | 0.04 | 1.3% | 168 | 0.11 | 5.3% | 89 | 0.17 | 4.7% | 78 | ||
| Peak Γstd (cm2/s) | 9.0 | 7.6% | 59 | 177.4 | 3.1% | 89 | 36.7 | 2.5% | 78 | ||
| Peak Γabs (cm2/s) | 144.0 | 0.8% | 69 | 211.2 | 5.9% | 99 | 264.3 | 2.2% | 108 | ||
| AΓ at peak Γabs () | 0.11 | 7.3% | 69 | 0.84 | 1.8% | 99 | −0.18 | 6.3% | 108 | ||
| Peak Hstd (m/s2) | 2.21 | 12.5% | 227 | 41.4 | 8.4% | 109 | 3.0 | 13.4% | 108 | ||
| Peak Habs (m/s2) | 27.6 | 0.8% | 69 | 66.8 | 2.8% | 99 | 44.2 | 1.2% | 88 | ||
| AH at peak Habs | −0.03 | 4.1% | 69 | 0.62 | 3.3% | 99 | 0.00 | 5.4% | 88 | ||
| Peak Hrel | 0.33 | 2.0% | 163 | 0.21 | 5.9% | 128 | 0.17 | 11.3% | 58 | ||
| Peak e | 0.10 | 12.3% | 138 | 0.17 | 5.7% | 129 | 0.21 | 0.0% | 98 | ||
Hemodynamic quantities correspond to peak systole. The numbers in square brackets indicate at which location the particular value was detected, in mm distance from the aortic valve.
The aorta of the normal control subject is characterized by low peak curvature (κ=0.45 cm−1) and effective torsion (κ·τ =0.16 cm−1), a Dean vortex in the ascending aorta with low circulation magnitude Γabs =144.0 cm2/s and helicity density magnitude Habs =27.6 m/s2, a vortex asymmetry of AΓ =0.11 and AH =−0.03 and a low peak retrograde flow fraction of QRFF =0.04 (Figure 5, right).
Segmentation and centerline of the neo-aorta in the HLHS patient exhibit a strong kinking at the highest point of the neo-aortic arch, 90 mm distal to the neo-aortic valve (Figures 2,3), with a prominent clockwise turning vortex visible in vicinity of the kinking (Figure 2). Curvature and effective torsion as parameters of the kinking reached maximum values of κ=0.53 cm−1 (κ·τ =0.41 cm−2) in the neo-aortic arch, 92 mm (88 mm) distal to the aortic valve and 7 mm (8 mm) proximal to the highest point of the neo-aortic arch, Table 1. Regions of high vorticity in vicinity of the kinking were related to regions of high TKE, as shown in Figure 3. In vicinity of the kinking, circulation, helicity density, cross-sectional turbulent kinetic energy density, peak turbulent kinetic energy density, and root mean-square of turbulent kinetic energy density coincide with maximum values, see Figure 4 and Table 1. Relative helicity density and flow displacement reach their maximum values 41–42 mm distal to the kinking. The peaks of both vorticity-related quantities (Γ,Hd) as well as the turbulence-related quantities (TKE, the root mean square TKERMS and peak values TKEmax) were asymmetrical with a steep increase at rising curvature in the ascending aorta and with a long tail at decreasing curvature in the descending aorta. TKE density reached its maximum of 275 J/m3 at a position 18 mm distal to the aortic arch (b), as shown in Figure 4. The vortex is represented by high helicity H and Γ, whereas the positive signs of peak values and asymmetries indicate the dominance of clockwise direction of rotation. The asymmetries AΓ (0.84) and AH (0.62) in the vicinity of peak circulation and helicity given in Table 1 more accurately describe the extent of dominance.
The VSARR patient exhibits a strong kinking with high curvature (κ=0.55 cm−1) and effective torsion (κ·τ=0.38 cm−2) at the distal anastomosis between the prosthesis of 6 cm length and native tissue. The in-plane flow pattern is a pair of counter-rotating cells, referred to as Dean vortices (5,34) 35 mm distal to the kinking, as in Figure 5 (left, C). The rotation-separated components Γ+, H+ and Γ-, H- shown in Figure 5 (left, panels 2 and 4) resolve the contributions of different directions of rotation and are compared with the magnitude of rotation Γabs, Habs. The asymmetries AΓ (−0.18) and AH (0.03) are low in the vicinity of peak circulation and helicity, as shown in Figure 5 (left, B), which can be interpreted as a pattern with an approximately symmetric pair of counter-rotating vortices. In association with the kinking, a peak retrograde flow fraction of QRFF=0.17 was detected.
Inter-observer variability ranged between 0% and 14% as listed in Table 1.
Discussion
We successfully developed a new analysis system for the comprehensive quantitative assessment and analysis of complex 4D Flow MRI data including secondary flow patterns. Multiple studies described the pathophysiological impact of secondary flow patterns (5-12) such as helicity. However, the parameters quantifying secondary flow patterns in blood vessels have not been well integrated in a uniform analysis scheme to allow a comprehensive diagnostic assessment and to facilitate the correlation of secondary flow patterns with anatomic anomalies as found in congenital heart diseases. The present study aims to address this clinical unmet need through MRI-based analysis of the flow.
Previous MRI studies with assessment of hemodynamics in blood vessels focused on the determination of distinct quantities derived from the velocity field map without a concordant longitudinally-resolved quantification of anatomic conditions (33,35).
Our approach allows an objective evaluation of the link between geometric changes and hemodynamics.
Several studies have applied manual positioning of a single or a few MPR planes within a vessel (9,10,36). However, successful detection of the peak values or other hemodynamic features with a single manually-positioned or sparsely-positioned MPR planes is less reliable as a-priori-knowledge about flow changes is usually not given. By applying the present method, peak values can easily be extracted from the data.
A recent study (23) reported that two counter-rotating helices, also known as Dean vortex, are typically found in the ascending aorta of healthy subjects. In contrast to healthy subjects, Dean vortices in VSARR patients are always associated with retrograde flow. We propose a method for visual grading, but emphasize on the lack of a quantitative analysis tool. Previous works on quantitative analysis of flow patterns with in-plane vortices in terms of circulation or helicity (11,33) did not take into account the possible cancellation effects due to counter-rotating pairs of vortices. Using suitable parameters, our method allows for quantification of helical flow patterns corroborating the previously described visual findings.
The disadvantages of the circulation (Eq. [6]) and helicity density (Eq. [9]) are their insensitivity to symmetric Dean flow patterns as shown in Figure 5. Symmetric Dean vortices cancel out due to opposite signs of the vortices. The components Γ+, H+ and Γ-, H- resolve the contributions of different directions of rotation and, in conjunction with circulation and helicity magnitudes Γabs, Habs, allow appropriate quantification of Dean vortices, see Figure 5 and Table 1. Numerical calculations suggest that different degrees of vortex asymmetries may develop depending on vessel torsion (17,37). As illustrated in Figure 5, we propose quantification of asymmetric Dean flow patterns by using circulation or helicity asymmetries (Eqs. [7] and [9]) thereby, a perfectly symmetric Dean flow pattern (A=0) can be distinguished from patterns with dominant clockwise (A>0), or anti-clockwise (A<0) vortices.
The Reynolds decomposition of the velocity field into the average and fluctuating components allows simplifying the Navier-Stokes equations to extract the flow’s laminar and turbulent contributions (38). Reynolds decomposition is practically adopted in 4D Flow MRI by providing the average velocity field and the intravoxel standard deviation (IVSD) corresponding to laminar and turbulent components as separate, complementary quantities of the same acquisition (27,28). Alternatively, vorticity measured by MRI only quantifies laminar components of the rotations (39). In the measured data, velocity and IVSD refer to the sub-voxel distributions, whereas vorticity describes a pattern of the environment related to the central voxel. Velocity, IVSD, and vorticity can be considered as complementary components from which secondary flow patterns are composed.
Based on the known technique of curved MPR (30) and using a vessel centerline, we describe a new method for computation of secondary hemodynamic parameters from the MPR of the three complementary building blocks: velocity, IVSD, and vorticity. This method allows an efficient use of computing power. The geometric distortion due to vessel curvature prevents Euclidean calculation of vorticity from velocity after MPR. Therefore, vorticity is calculated before MPR. Combination of velocity and vorticity after MPR enables the calculation of average cross-sectional vorticity, circulation, helicity density and relative helicity density as well as all basic parameters based on through-plane velocities.
The new method applies the known technique of curved MPR to a multi-dimensional feature space and simultaneously uses the centerline for both MPR and quantification of curvilinearity to facilitate analyses involving hemodynamic and anatomic quantification. As mentioned before, conventional circulation and helicity density are not suitable parameters for quantification of Dean flow pattern. We introduced the use of rotation-separated components as well as circulation and helicity density magnitudes in conjunction with circulation and helicity density asymmetries for an appropriate quantification of Dean vortices.
Limitations
Our method can currently only be applied for determination of hemodynamic and anatomic parameters in large blood vessels. Quantification of other parameters particularly in small blood vessels and in the heart is in process.
Our method does not take into account the aortic wall motion during the blood vessel segmentation. However, the segmentation algorithm can be improved without affecting other components of the platform as they do not require a static vessel segmentation in all time frames. Supra-aortic vessels may partly affect the quantification of the aortic arch if the resampling region is larger than the arch. Thus, it is recommended that the size of the resampling region should be adjusted as close as possible.
Conclusions
Our novel method allows systematic quantification of a large number of flow and anatomic parameters for clinical decision-making. We showed the performance of our method using three clinical test cases to reveal inter-dependencies between local anatomic and hemodynamic parameters along a blood vessel path. The separate consideration of rotational directions allows quantification of Dean flow patterns based on circulation and helicity density.
Acknowledgments
The authors would like to thank Mrs. Traudel Hansen for her support with patient management. The authors also thank Ms. Christien Boll for her support with the determination of inter-observer deviations.
Funding: This work was partially supported by an experienced researcher award from the Alexander von Humboldt Foundation to Prof. Kheradvar.
Footnote
Provenance and Peer Review: This article was commissioned by the Guest Editors (Yskert von Kodolitsch, Harald Kaemmerer, Koichiro Niwa) for the series “Current Management Aspects in Adult Congenital Heart Disease (ACHD): Part IV” published in Cardiovascular Diagnosis and Therapy. The article has undergone external peer review.
Reporting Checklist: The authors have completed the MDAR reporting checklist. Available at http://dx.doi.org/10.21037/cdt-20-767
Data Sharing Statement: Available at http://dx.doi.org/10.21037/cdt-20-767
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/cdt-20-767). The series “Current Management Aspects in Adult Congenital Heart Disease (ACHD): Part IV” was commissioned by the editorial office without any funding or sponsorship. DDG reports having a patent application 18752420.2 - 1010 pending. AK reports grants from Alexander von Humboldt Foundation, during the conduct of the study. The authors have no other conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by institutional ethics board of Kiel University’s Faculty of Medicine (A168/07) and informed consent was taken from all individual participants.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- O'Donnell M. NMR blood flow imaging using multiecho, phase contrast sequences. Med Phys 1985;12:59-64. [Crossref] [PubMed]
- Markl M, Chan FP, Alley MT, et al. Time-resolved three-dimensional phase-contrast MRI. J Magn Reson Imaging 2003;17:499-506. [Crossref] [PubMed]
- Markl M, Frydrychowicz A, Kozerke S, et al. 4D flow MRI. J Magn Reson Imaging 2012;36:1015-36. [Crossref] [PubMed]
- Sträter A, Huber A, Rudolph J, et al. 4D-Flow MRI: Technique and Applications. Rofo 2018;190:1025-35. [Crossref] [PubMed]
- Liu X, Sun A, Fan Y, et al. Physiological significance of helical flow in the arterial system and its potential clinical applications. Ann Biomed Eng 2015;43:3-15. [Crossref] [PubMed]
- Ha H, Ziegler M, Welander M, et al. Age-related vascular changes affect turbulence in aortic blood flow. Front Physiol 2018;9:36-45. [Crossref] [PubMed]
- Ha H, Kim GB, Kweon J, et al. Turbulent Kinetic Energy Measurement Using Phase Contrast MRI for Estimating the Post-Stenotic Pressure Drop: In Vitro Validation and Clinical Application. PLoS One 2016;11:e0151540. [Crossref] [PubMed]
- Ge L, Lassab GS. Turbulence in the Cardiovascular System: Aortic Aneurysm as an Illustrative Example. Berlin Heidelberg: Springer-Verlag 2009:319.
- Sigovan M, Hope MD, Dyverfeldt P, et al. Comparison of four-dimensional flow parameters for quantification of flow eccentricity in the ascending aorta. J Magn Reson Imaging 2011;34:1226-30. [Crossref] [PubMed]
- Ayaon-Albarran A, Fernandez-Jimenez R, Silva-Guisasola J, et al. Systolic flow displacement using 3D magnetic resonance imaging in an experimental model of ascending aorta aneurysm: impact of rheological factors. Eur J Cardiothorac Surg 2016;50:685-92. [Crossref] [PubMed]
- Rickers C, Kheradvar A, Sievers HH, et al. Is the Lecompte technique the last word on transposition of the great arteries repair for all patients? A magnetic resonance imaging study including a spiral technique two decades postoperatively. Interact Cardiovasc Thorac Surg 2016;22:817-25. [Crossref] [PubMed]
- Sievers HH, Putman LM, Kheradvar A, et al. 4D flow streamline characteristics of the great arteries twenty years after Lecompte and direct spiral arterial switch operation (DSASO) in simple TGA. Glob Cardiol Sci Pract 2016;2016:e201629. [Crossref] [PubMed]
- Constantinides P. Importance of the endothelium and blood platelets in the pathogenesis of atherosclerosis. Triangle 1976;15:53-61. [PubMed]
- Golan DE. Principles of Pharmacology: The Pathophysiologic Basis of Drug Therapy. Alphen aan den Rijn: Wolters Kluwer Health, 2009:1020.
- Mehta V, Tzima E. Cardiovascular disease: A turbulent path to plaque formation. Nature 2016;540:531-2. [Crossref] [PubMed]
- Liu X, Pu F, Fan Y, et al. A numerical study on the flow of blood and the transport of LDL in the human aorta: the physiological significance of the helical flow in the aortic arch. Am J Physiol Heart Circ Physiol 2009;297:H163-170. [Crossref] [PubMed]
- Liu X, Fan Y, Deng X. Effect of Spiral Flow on the Transport of Oxygen in the Aorta: A Numerical Study. Ann Biomed Eng 2010;38:917-26. [Crossref] [PubMed]
- Javadzadegan A, Simmons A, Barber T. Spiral blood flow in aorta-renal bifurcation models. Comput Methods Biomech Biomed Engin. 2016;19:964-76. [Crossref] [PubMed]
- Tse KM, Chang R, Lee HP, et al. A computational fluid dynamics study on geometrical influence of the aorta on haemodynamics. Eur J Cardiothorac Surg 2013;43:829-38. [Crossref] [PubMed]
- Misfeld M, Scharfschwerdt M, Sievers HH. A novel, form-stable, anatomically curved vascular prosthesis for replacement of the thoracic aorta. Ann Thorac Surg 2004;78:1060-3. [Crossref] [PubMed]
- Cheng Z, Kidher E, Jarral OA, et al. Assessment of hemodynamic conditions in the aorta following root replacement with composite valve-conduit graft. Ann Biomed Eng 2016;44:1392-404. [Crossref] [PubMed]
- Dean W, Hurst J. Note on the motion of fluid in a curved pipe. Mathematika 1959;6:77-85. [Crossref]
- Oechtering TH, Sieren MM, Hunold P, et al. Time-resolved 3-dimensional Magnetic Resonance Phase Contrast Imaging (4D Flow MRI) Reveals Altered Blood Flow Patterns in the Ascending Aorta of Patients With Valve-Sparing Aortic Root Replacement. J Thorac Cardiovasc Surg. 2020;159:798-810.e1. [Crossref] [PubMed]
- Yabrodi M, Mastropietro CW. Hypoplastic left heart syndrome: from comfort care to long-term survival. Pediatr Res 2017;81:142-9. [Crossref] [PubMed]
- Dyverfeldt P, Bissell M, Barker AJ, et al. 4D flow cardiovascular magnetic resonance consensus statement. J Cardiovasc Magn Reson 2015;17:72-90. [Crossref] [PubMed]
- Anderson JD. Computational Hemodynamics – The Basics with Applications. New York: Tata-Mcgraw Hill, 1995:563.
- Dyverfeldt P, Sigfridsson A, Kvitting JP, et al. Quantification of intravoxel velocity standard deviation and turbulence intensity by generalizing phase-contrast MRI. Magn Reson Med 2006;56:850-8. [Crossref] [PubMed]
- Dyverfeldt P, Kvitting JP, Sigfridsson A, et al. Assessment of fluctuating velocities in disturbed cardiovascular blood flow: in vivo feasibility of generalized phase-contrast MRI. J Magn Reson Imaging 2008;28:655-63. [Crossref] [PubMed]
- Nielson GM, Hamann B. The asymptotic decider: resolving the ambiguity in marching cubes. In Proceedings of the 2nd conference on Visualization 1991, Los Alamitos, CA, USA, 1991:83-91.
- Rubin GD, Napel S, Leung AN. Volumetric analysis of volumetric data: achieving a paradigm shift. Radiology 1996;200:312-7. [Crossref] [PubMed]
- Robert Hagan. Numerical Methods for Isosurface Volume Rendering. Virginia Tech, 2009:1-4.
- Hess AT, Bissell MM, Glaze SJ, et al. Evaluation of Circulation, Γ, as a quantifying metric in 4D flow MRI. J Cardiovasc Magn Reson 2013;15:E36. [Crossref]
- Lorenz R, Bock J, Barker AJ, et al. 4D flow magnetic resonance imaging in bicuspid aortic valve disease demonstrates altered distribution of aortic blood flow helicity. Magn Reson Med 2014;71:1542-53. [Crossref] [PubMed]
- Dennis SCR, Ng M. Dual solutions for steady laminar-flow through a curved tube. Q J Mech Appl Math 1982;35:305. [Crossref]
- Sigovan M, Dyverfeldt P, Wrenn J, et al. Extended 3D approach for quantification of abnormal ascending aortic flow. Magn Reson Imaging 2015;33:695-700. [Crossref] [PubMed]
- von Knobelsdorff-Brenkenhoff F, Trauzeddel RF, Barker AJ, et al. Blood flow characteristics in the ascending aorta after aortic valve replacement - a pilot study using 4D-flow MRI. Int J Cardiol 2014;170:426-33. [Crossref] [PubMed]
- Yamamoto K, Aribowo A, Hayamizu Y, et al. Visualization of the flow in a helical pipe. Fluid Dyn Res 2002;30:251-67. [Crossref]
- Adrian RJ, Christensen KT, Liu ZC. Analysis and interpretation of instantaneous turbulent velocity fields. Exp Fluids 2000;29:275-90. [Crossref]
- Kheradvar A, Pedrizzetti G. Vortex Formation in the Cardiovascular System. Berlin Heidelberg: Springer-Verlag, 2012:159.


